Introducción a los Lenguajes formales

Introducción.

Un lenguaje es un conjunto de símbolos (o palabras) y métodos para estructurar y combinar dichos símbolos, también recibe el nombre de idioma y consta de todos los símbolos válidos por dicho lenguaje y métodos. Esta clase de lenguajes recibe el nombre de lenguaje natural.

Existen lenguajes de menor capacidad para simular y modelar lenguajes naturales, como el binario, Java, C, Basic o Pascal que se utilizan con las computadoras a estos se les llama LENGUAJES FORMALES.

Es difícil modelar un lenguaje natural con todas sus reglas y palabras, por esto se utilizan lenguajes formales para establecer la comunicación con las computadoras y sus periféricos. Se tiene lenguajes para controlar sistemas de producción automatizados en empresas, y para programar robots, controlar aviones o manejar base de datos.

El problema para simular un lenguaje natural por medio de un lenguaje formal radica no solamente en la estructuración correcta de las palabras (sintaxis) sino también en el significado de una palabra o frase (semántica) que muchas veces varía de persona a persona, dependiendo del lugar, contexto o estado de ánimo.

Gramática y lenguajes formales.

Lenguaje L (G). Este tipo de lenguaje se basa en la gramática, así como el las reglas o métodos para la creación de palabras propias del lenguajes, y consiste en una (G) gramática con todos los arreglos que se pueden obtener a partir del estado inicial (s) y las composiciones (c).

Estructuración de las gramáticas.

La gramática G= {∑, N, T, s, c} es el sistema que permite establecer las reglas que han de aplicarse a un lenguaje:

∑: es el alfabeto o conjunto de símbolos con el cual se forman palabras de un lenguaje.

N: conjunto de símbolos no terminales en un lenguaje.

T: conjunto de símbolos terminales.

s: estado inicial.

c: conjunto de composiciones o reglas que se deben usar para la estructuración de las palabras válidas en el lenguaje.

Un símbolo es cualquier carácter o figura, por ejemplo: a, b, p, 3, 5, #, &, @, etcétera.

Ejemplo: ∑= {a, b, c, d,…, z}

L (G)= {hola, conejo, pera, piña,…,}

Con los símbolos del alfabeto es posible estructurar palabras de un lenguaje, siguiendo ciertas reglas para su correcta estructuración.

En una gramática los símbolos terminales (T) se indican por medio de números o letras minúsculas, los no terminales (N) por letras mayúsculas o la letra s para indicar que se trata del símbolo inicial.

Las palabras válidas en un lenguaje dependen del alfabeto y de las composiciones (c), estas están integradas por símbolos terminales y no terminales.

Ejemplo: ∑= {a, g, h, i, l, m, o, r}

Cuyas composiciones (c) son:

s—>hAB —>rD             F—>gC

A —>oBD —>mE            C—> a

B —>1C                         E —>iF

Para que una palabra se considere parte de un lenguaje deberá estar formada solamente por símbolos terminales, ya que los símbolos no terminales forzosamente llevaran a integrar nuevos símbolos terminales y símbolos no terminales.

Clasificación de las gramaticales-

Las gramáticas se pueden clasificar como:

Tipo 0: si no se pone ninguna restricción a las composiciones de G.

Tipo 1: si para cualquier composición d₁ —> d₂ de la gramática G, la longitud de símbolos de la izquierda de la composición (d₁) es menor o igual a la longitud de símbolos de la derecha (d₂).

Tipo 2: si el lado izquierdo de cada composición es un símbolo no terminal y el lado derecho consta de uno o más símbolos terminales y/o no terminales.

Tipo 3: si el lado izquierdo de la composición es un símbolo no terminal y el lado derecho tiene uno o más símbolos, incluyendo a lo más un símbolo no terminal.

A las gramáticas 0 y 1 también se les conoce como Sensibles al contexto. Son muy complicadas, difíciles de analizar y estudiar.

La gramática tipo 2 recibe el nombre de Libre de contexto. Este se usa actualmente para la creación de lenguajes formales, tiene relación con los autómatas finitos, autómatas de pila y máquinas de Turing.

La gramática tipo 3 o también llamada Regular, tiene reglas simples de sustitución y generación de palabras de un lenguaje. Esta sustituye un símbolo no terminal por uno terminal. La gramática regular tiene una relación con los autómatas finitos.

Una gramática regular es, una gramática libre de contexto y también sensible al contexto.

Ejemplo=Considérese la siguiente gramática G en donde:

T= {a, b} Conjunto de símbolos terminales.

N = {s, A, B} Conjunto de símbolos no terminales, donde s es el símbolo inicial.

Composiciones:

s —>aA A —>aaB        AB —>sB

AbB —> aA       B —>bAa—> a

Esta gramática es sensible al contexto, ya que no presenta ninguna restriccióna las composiciones. Una característica es que el número de símbolosdel lado izquierdo de la composición AbB —> aA es mayor que el número de símbolos del lado derecho, cosa que no es permitido en ninguna de las demásgramáticas.

Representación de las gramáticas.

Existen gramáticas regulares, libres de contexto y sensibles al contexto, cada una tiene su propia forma de representación.

Gramáticas regulares. Se representan principalmente por medio de autómatas finitos los cuales son generadores de palabras de un lenguaje, donde se genera comenzando en el símbolo inicial y terminando como una cadena de símbolos terminales y no contienen ningún símbolo terminal.

Se puede decir que la gramática de un lenguaje regular es semejante a un autómata finito, se representa en forma gráfica cada una de las composiciones de la gramática teniendo en cuenta que los símbolos no terminales se encierran en círculos y los símbolos terminales son las etiquetas de las aristas del autómata finito.

Ejemplo=Sea la gramática G, en donde:

                                                                       

Gramáticas libres de contexto. Este tipo son las más usadas en la elaboración de compiladores, traductores e intérpretes, y se pueden representar por medio de árboles de derivación, representación BNF y diagramas sintácticos.

Representación mediante árboles de derivación. Para determinar si una palabra pertenece a un lenguaje por el método de árboles de derivación es semejante al desarrollo por medio de composiciones, en este caso se estructura un árbol teniendo como raíz de ese árbol al símbolo inicial s y colocando como hijos a los signos del derecho de la composición. El árbol se termina de estructurar cuando todas sus hojas son símbolos terminales de izquierda a derecha es una palabra que pertenece al lenguaje L (G).

Ejemplo: la gramática libre de contexto G=

 Representación BNF (Backus-Naur). Se mencionó con anterioridad que la gramática libre de contexto se utiliza con frecuencia para la representación de lenguajes formales como C, Pascal, Basic, etc. La representación BNF'es un buen ejemplo de ello.

Ejemplo: Sea la gramática libre de contexto G:

T = {x, y}

N = {s, A, B, C}

Composiciones:

s  —>xB   B  —>yxCC  —>BxA

A  —>xBy B —>yyCC  —>xy

A —>CBxB  —> xA  —>y

La representación de la gramática por medio de BNF es:

s::=xB B: := yxC /yyC / x

A : :=xBy / CBx / yC::=BxA / xy

Algunas veces en la representación BNF los símbolos no terminales empiezancon “<” terminan con “> ” y la flecha (—>) de una composición se indica con “ : :=” . Por ejemplo, la composicións->AB se representa de la siguiente manera:

<s>::=<A><B>

Composiciones de la forma s  —> AB,  s  —>abB, s —>bAa,s ->b son equivalentes a

s : := <A><B> / ab <B> / b <A> a/ b.

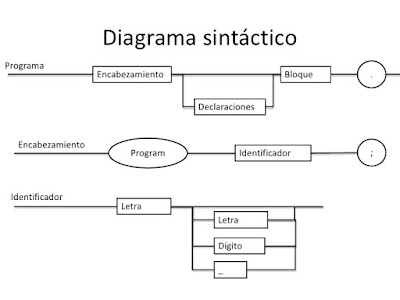
Diagramas sintácticos. Es una forma gráfica para representar una gramática por medio de gráficas dinámicas que permiten determinar en forma más ilustrativa si una palabra pertenece a un lenguaje; a esta gráfica se le conoce como diagrama sintáctico o diagrama de sintaxis. En un diagrama sintáctico los símbolos no terminales se representan dentro de un cuadro, y los símbolos terminales se encierran dentro de un círculo.

El diagrama sintáctico que representa a la composición

                                                

 

Autómatas finitos.

Todo proceso que recibe una o varias entradas, que se transforman y emiten una salida recibe el nombre de sistema. Existen sistemas muy complejos, como los sistemas de los vivos; por ejemplo una planta recibe como entrada agua, sales minerales, oxígeno y luz solar, procesa esas entradas y emite como salida hojas, tallos, flores y frutos. Parece muy sencillo, sin embargo no lo es ya que de acuerdo con las entradas, cantidad y calidad de elementos, así como el medio ambiente que rodea a la planta, puede tener mejores flores y frutos.

Los autómatas finitos reciben como entrada información que procesan, y emiten salida. Un autómata finito recibe una palabra, la cual procesa, por medio de un recorrido a través de los diferentes estados que integran el autómata, si al final del procesamiento el recorrido termina en un estado o posición de aceptación, se dice que la palabra forma parte del lenguaje.

Terminología básica. Las gramáticas son parte esencial de los lenguajes regulares y los autómatas finitos (AF) son una representación grafica de los lenguajes regulares. Es conveniente tener en cuenta algunos conceptos importantes que permiten la manipulación correcta de los lenguajes regulares y los autómatas finitos. Una palabra que pertenece a un lenguaje L (G) realmente es una cadena de símbolos o caracteres, y por esto la relación existente entre los símbolos, cadenas, lenguajes, alfabetos y gramáticas es importante.

Cadena.Ésta consiste en una secuencia de símbolos yuxtapuestos (se coloca uno seguido del otro).

∑ = {0, 1, 2}   

w= 0    x = 02    y =011    z= 12012

En este caso w, x, y, z son cadenas formadas con símbolos del alfabeto ∑.

Cadena vacía. Es aquella que no tiene símbolos. Aquí se tiene que Ɛw = wƐ y ƐƐ = Ɛ.

Si w = pera, entonces

Ɛw = pera = wƐ.

Inversa de una cadena (w¹). Es la cadena que se obtiene al escribir los caracteres en forma invertida.

Sea w - Hola, entonces

W¹ = (Hola)¹ = (ola)¹H = (la)¹oH = (a )¹loH = (ϵ)¹loH = aloH 

Cadena elevada a una potencia (wⁿ). Si n es un elemento del conjunto de números naturales (n ϵ N) y w es una cadena, entonces:

W⁰ = e (cadena vacía)

 W¹ = ww⁰

W² = ww¹ = www⁰

W³ = ww² = www¹ = wwww⁰

Wⁿ = ww^n-1

Cerradura de Kleene elevada a una potencia o cerradura estrella (L^*). Es el lenguaje con todas las cadenas que se pueden formar con el alfabeto (∑).

 ∑ = {0, 1}

 ∑* = {0, 1, 00, 01, 10, 11, 000, 100, 101, 110, 111, 0000, 0001, 0010,...}

Cerradura estrella sobre un lenguaje (L⁺). Es la unión de todos los lenguajes potencial de L desde n = 0 hasta infinito (n ϵ N), que se puede formar con el alfabeto (∑).

∑ = {a, b}, L = {abb};

L^*=L⁰ ᴗ L¹ ᴗ... ᴗ L^∞ = {Ɛ} ᴗ {abb} ᴗ {abbabb} ᴗ... ᴗ {abb}^∞

L^*= {Ɛ, abb, abbabb, abbabbabb,...}

Cerradura positiva de un lenguaje (L⁺). Es la unión de todos los lenguajes potencias de L, desde n = 1 hasta infinito, que se puede formar con el alfabeto (∑).

 ∑= {a, b}, L = {abb};

 L+ = L¹ ᴗ L² ᴗ... ᴗ L^∞ = {abb} ᴗ {abbabb)} ᴗ... ᴗ {abb}^∞

 L+ = {abb, abbabb, abbabbabb,...}

Inversa de un lenguaje (L^I). Es el lenguaje que se obtiene al escribir los elementos de un lenguaje en forma invertida.

L= {Morelia, Michoacán}; ∑ ={a, b, c,…z}

L¹⁼ {ailoreM, nácaohciM}.

Lenguajes regulares. Con el alfabeto ∑ es posible formar una gran cantidad de lenguajes, pero no existe un método efectivo para saber cuántos de ellos son regulares. Todos los lenguajes sobre ∑ son sublenguajes del lenguaje universo ∑^* , se utilizarán algunas propiedades de los lenguajes para determinar cuáles de ellos son regulares. El conjunto de lenguajes regulares sobre ∑ son:

Ø  El lenguaje vacío Ө.  

Ø  El lenguaje que contiene la cadena vacía como único elemento (Ɛ).

Ø  El lenguaje unitario {a}es regular Ɐ a ϵ ∑.

Ø  Si L y M son lenguajes regulares, también lo son el lenguaje que resulta de la unión (L ᴗ M), la concatenación (LM), la potenciación (Lⁿ Mⁿ) y la cerradura de Kleene (L^*).

Ø  Ningún otro lenguaje ∑es regular.

Expresiones regulares. Es una nueva forma de expresar los lenguajes regulares y tiene la finalidad de facilitar la manipulación y simplificación de los mismos.

Lenguaje regular	Expresión regular
{a}	a
{ϵ}	Ɛ
Ǿ*	Ɛ
{a}+	a+
{a}*	a*
{ab}	ab
{a}ᴗ{b}= {a, b}	aᴗb

De esta manera el lenguaje {a, bc}^*{Ɛ, aab}Ǿ{c}sobre ∑= {a, b, c}, se puede indicar por medio de una expresión (aᴗbc)*(Ɛᴗaab) Ɛc.

Autómatas finitos (AF). Los AF constan de 5 elementos fundamentales:

1.    Alfabeto ∑.

2.    Conjunto de estados E.

3.    Estado inicial s.

4.    Conjunto de estados finales F.

5.    Una función: Ex ∑ ----> E que permite determinar cuál es el estado siguiente.

Diagrama de transición. En los diagramas de transición, los estados se representan por medio de un círculo con el nombre del estado dentro de él. Los estados de aceptación o finales se distinguen por el círculo doble, las transiciones se representan por aristas, se etiquetan con un símbolo del alfabeto. El estado inicial se distingue porque se hace incidir sobre él una flecha. 

Autómatas finitos determinísticos (afd).

Se dice que un autómata finito es determinístico si  por medio de la función de transición: Ex∑ à E es posible determinar claramente cuál es el estado siguiente. El autómata anteriormente visto es un AFD, ya que cuando se está en un estado cualquiera y se tiene un símbolo del alfabeto, es posible determinar claramente cuál es el estado siguiente.

También es un AFD el siguiente, en donde:

∑ = {x, y}

 E = {q₀, q₁, 0₂, q₃, q₄}

 s = q₀

F={q₃}

Con la tabla de transiciones, dicho AFD queda indicado completamente de la sig., manera:

s=q₀ y F = {q₃}

8	X	y
q0	q1	q4
q1	q1	q2
q2	q2	q3
q4	q4	q4

Dicho AFD acepta cadenas de caracteres que comienzan con xy terminan con yx.

Automatas finitos no determinísticos (afn).

La diferencia fundamental entre autómatas finitos determinísticos (AFD) y un autómata finito no determinístico (AFN), es que en el AFN la función de estado siguiente no conduce un estado único determinado. En algunas de ellas el juego se interrumpe cuando ha trascurrido cierto tiempo, en otras porque el usuario llegó a la meta. Todo esto y otros estados se deberán considerar en una máquina de estado finito.

Una máquina de estado finito, en donde M= {E, A, B, s, 8, a} se define como un sistema que cuenta con un número finito de estados E, que acepta un conjunto finito de entradas A y que puede tener un número finito de salidas B, además tiene un estado inicial s. Cuenta también con dos funciones: 8, también llamada función de estado siguiente y se define con c: E x A E (depende del estado y la entrada, su salida es un estado siguiente) y la función 8 denominada también función de salida está definida como 8: E x A —> B (depende del estado y la entrada, y se obtiene como resultado un elemento del conjunto de salida B).

Ejemplo: La máquina para sumar dos cantidades de base 3 es como se muestra a continuación:

10=1                              21=0                       22=2

11=2                              12=0                       21=1

20=2                              22=1                       20=0

00=0                              00=1                       12=1

01=1                              01=2                       11=0

02=2                              10=2                       02=0

Esta máquina de estado finito está integrada por:

E = [e₀, e₁)                                                                                 Conjunto de estados.

A = {00, 01, 02, 10, 11, 12, 20, 21, 22}                                      Conjunto finito de entradas.

B = {0, 1, 2}                                                                               Conjunto de salidas.

 s = e₀ Estado inicial.

Se observa claramente que ninguno de los estados del conjunto E es de aceptación, porque las máquinas de estado finito no tienen estados aceptados. El conjunto E={e₀, e₁} tiene dos estados, e₀ que a su vez es el esta do inicial y el estado en el que no hay ningún acarreo. El estado e2 es la posición en que se le suma el acarreo a los nuevos bits sumados y permanece ahí, siempre y cuando la suma de los bits nuevos y el acarreo generen un nuevo acarreo, en caso contrario regresará al estado e_0.

El conjunto A contiene todas las combinaciones posibles que se pueden presentar cuando se suman dos cantidades en binario {00, 01, 02, 10, 11, 12, 20, 21, 22}.

El conjunto B contiene todos aquellos símbolos de salida posibles {0, 1, 2}.

Equivalencia entre autómatas finitos y máquinas de estado finito.

Un autómata finito se puede considerar como una máquina de estado finito. Recordando que los autómatas tienen los elementos AF = (X, E, F, s, 8) y que los de las máquinas de estado finito son M = {E, A, B, a, 8, a}, se puede observar cierta equivalencia entre ellos que permite determinar la máquina de estado finito equivalente de un autómata finito y viceversa. La equivalencia entre elementos es como sigue:

• El alfabeto finito de símbolos de un autómata, equivale al conjunto de símbolos finitos de entrada de una máquina de estado finito X = A.
• El conjunto de estados en un AF, equivale al conjunto de estados en una máquina de estado finito E=E.
• El conjunto de estados aceptados en un AF, equivale a las transiciones que inciden en un estado y cuyo símbolo de salida es 1.
• La función de estado siguiente 5 en un AF, equivale a la función de estado siguiente 5 en una máquina de estado finito 8 = 5.
• El estado inicial s en un AF, equivale al estado inicial s de la máquina de estado finito s= s.
• En los autómatas finitos no existe la función de salida o de una máquina, ya que para determinar si una palabra pertenece a un lenguaje se tienen los estados aceptados.

La máquina de Turing.

La maquina consiste en una cinta que se extiende de manera infinita, en donde se escribe o se lee información por medo de una cabeza de lectura-escritura. La máquina de Turing es un conjunto de elementos MT= (E, ∑, A, s, b, F, 8) en donde:

E: Conjunto finito de estados.

∑: Conjunto de símbolos de entrada.

A: Alfabeto de la cinta.

 s: estado inicial s ϵ E.

 b: Símbolo blanco, el cuál es un elemento del alfabeto de la cinta, pero no del conjunto de símbolos de entrada; b ϵ A, b ϵ ∑

F: Conjunto de estados de aceptación.

8: Función de transición en donde 8: ExA->ExAx {D,I}.

En la función de transición entra el estado actual en donde se encuentra la MT (e) y un símbolo de la cinta (o) para obtenerse con dicha función una terna conformada por el estado siguiente (f), el símbolo escrito en la cinta (a) y un movimiento de la cinta (m)

8(e, a) = (f; a, m).